Iterative Closest Point coregistration

Some DEMs may for one or more reason be erroneously rotated in the X, Y or Z directions. Established coregistration approaches like Nuth and Kääb (2011) work great for X, Y and Z translations, but rotation is not accounted for at all.

Iterative Closest Point (ICP) is one method that takes both rotation and translation into account. It is however not as good as Nuth and Kääb (2011) when it comes to sub-pixel accuracy. Fortunately, xdem provides the best of two worlds by allowing a combination of the two.

Reference: Besl and McKay (1992).

import matplotlib.pyplot as plt
import numpy as np

import xdem

Let’s load a DEM and crop it to a single mountain on Svalbard, called Battfjellet. Its aspects vary in every direction, and is therefore a good candidate for coregistration exercises.

dem = xdem.DEM(xdem.examples.get_path("longyearbyen_ref_dem"))

subset_extent = [523000, 8660000, 529000, 8665000]
dem.crop(subset_extent)

Let’s plot a hillshade of the mountain for context.

xdem.terrain.hillshade(dem).show(cmap="gray")

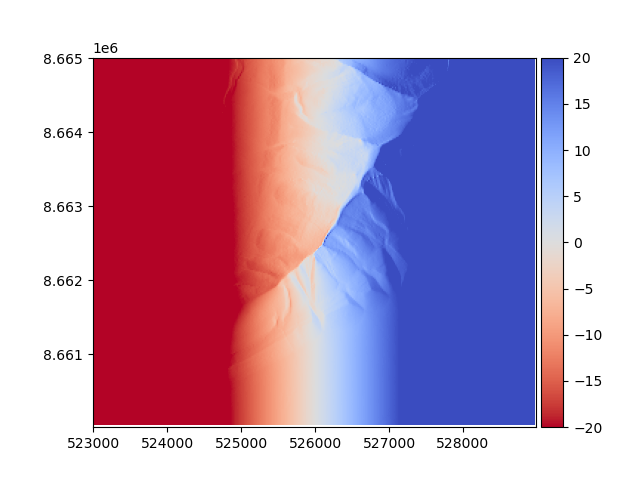
To try the effects of rotation, we can artificially rotate the DEM using a transformation matrix. Here, a rotation of just one degree is attempted. But keep in mind: the window is 6 km wide; 1 degree of rotation at the center equals to a 52 m vertical difference at the edges!

rotation = np.deg2rad(1)
rotation_matrix = np.array(
    [
        [np.cos(rotation), 0, np.sin(rotation), 0],
        [0, 1, 0, 0],
        [-np.sin(rotation), 0, np.cos(rotation), 0],
        [0, 0, 0, 1],
    ]
)

# This will apply the matrix along the center of the DEM
rotated_dem_data = xdem.coreg.apply_matrix(dem.data.squeeze(), transform=dem.transform, matrix=rotation_matrix)
rotated_dem = xdem.DEM.from_array(rotated_dem_data, transform=dem.transform, crs=dem.crs, nodata=-9999)

We can plot the difference between the original and rotated DEM. It is now artificially tilting from east down to the west.

diff_before = dem - rotated_dem
diff_before.show(cmap="coolwarm_r", vmin=-20, vmax=20)
plt.show()

As previously mentioned, NuthKaab works well on sub-pixel scale but does not handle rotation. ICP works with rotation but lacks the sub-pixel accuracy. Luckily, these can be combined! Any xdem.coreg.Coreg subclass can be added with another, making a xdem.coreg.CoregPipeline. With a pipeline, each step is run sequentially, potentially leading to a better result. Let’s try all three approaches: ICP, NuthKaab and ICP + NuthKaab.

approaches = [
    (xdem.coreg.ICP(), "ICP"),
    (xdem.coreg.NuthKaab(), "NuthKaab"),
    (xdem.coreg.ICP() + xdem.coreg.NuthKaab(), "ICP + NuthKaab"),
]


plt.figure(figsize=(6, 12))

for i, (approach, name) in enumerate(approaches):
    approach.fit(
        reference_dem=dem,
        dem_to_be_aligned=rotated_dem,
    )

    corrected_dem = approach.apply(dem=rotated_dem)

    diff = dem - corrected_dem

    ax = plt.subplot(3, 1, i + 1)
    plt.title(name)
    diff.show(cmap="coolwarm_r", vmin=-20, vmax=20, ax=ax)

plt.tight_layout()
plt.show()

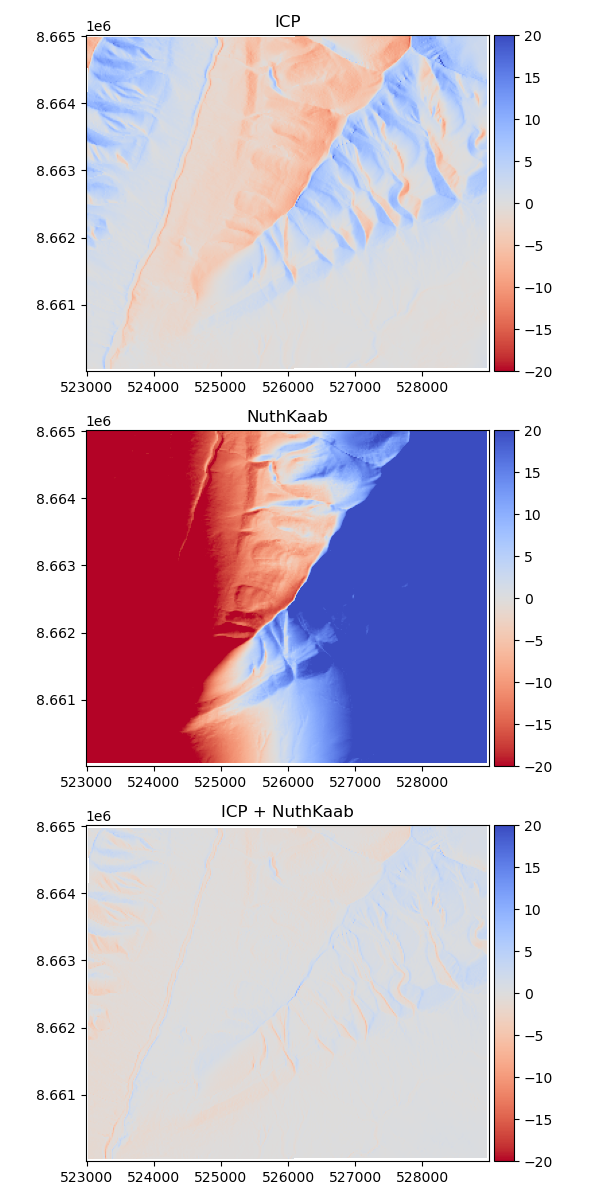
The results show what we expected:

• ICP alone handled the rotational offset, but left a horizontal offset as it is not sub-pixel accurate (in this case, the resolution is 20x20m).

• NuthKaab barely helped at all, since the offset is purely rotational.

• ICP + NuthKaab first handled the rotation, then fit the reference with sub-pixel accuracy.

The last result is an almost identical raster that was offset but then corrected back to its original position!