Spatial correlation of errors

Digital elevation models have errors that are spatially correlated due to instrument or processing effects. Here, we rely on a non-stationary spatial statistics framework to estimate and model spatial correlations in elevation error. We use a sum of variogram forms to model this correlation, with stable terrain as an error proxy for moving terrain.

Reference: Hugonnet et al. (2022), Figure 5 and Equations 13–16.

import geoutils as gu

import xdem

We load a difference of DEMs at Longyearbyen, already coregistered using Nuth and Kääb (2011) as shown in the Nuth and Kääb coregistration example. We also load the glacier outlines here corresponding to moving terrain.

dh = xdem.DEM(xdem.examples.get_path("longyearbyen_ddem"))
glacier_outlines = gu.Vector(xdem.examples.get_path("longyearbyen_glacier_outlines"))

Then, we run the pipeline for inference of elevation heteroscedasticity from stable terrain (Note: we pass a random_state argument to ensure a fixed, reproducible random subsampling in this example). We ask for a fit with a Gaussian model for short range (as it is passed first), and Spherical for long range (as it is passed second):

(
    df_empirical_variogram,
    df_model_params,
    spatial_corr_function,
) = xdem.spatialstats.infer_spatial_correlation_from_stable(
    dvalues=dh, list_models=["Gaussian", "Spherical"], unstable_mask=glacier_outlines, random_state=42
)

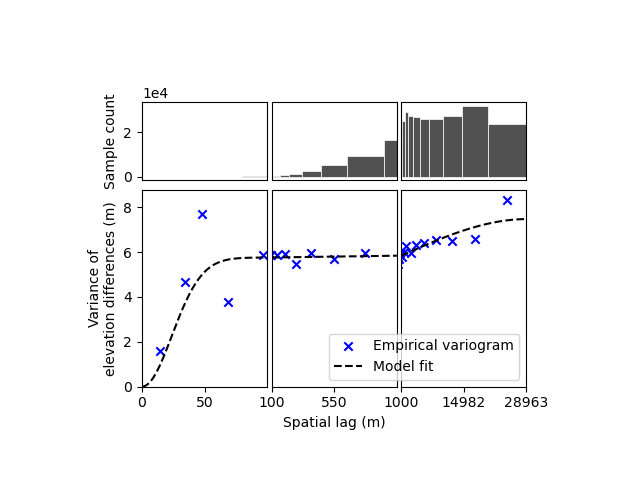
The first output corresponds to the dataframe of the empirical variogram, by default estimated using Dowd’s estimator and the circular sampling scheme of skgstat.RasterEquidistantMetricSpace (Fig. S13 of Hugonnet et al. (2022)). The lags columns is the upper bound of spatial lag bins (lower bound of first bin being 0), the exp column is the “experimental” variance value of the variogram in that bin, the count the number of pairwise samples, and err_exp the 1-sigma error of the “experimental” variance, if more than one variogram is estimated with the n_variograms parameter.

df_empirical_variogram

	exp	lags	count	err_exp
0	2.346189	28.284271	10	NaN
1	4.933423	40.000000	35	NaN
2	6.397679	56.568542	45	NaN
3	5.126353	80.000000	80	NaN
4	5.483011	113.137085	161	NaN
5	5.741364	160.000000	323	NaN
6	5.883358	226.274170	699	NaN
7	5.552374	320.000000	1233	NaN
8	6.269101	452.548340	2648	NaN
9	6.137944	640.000000	5019	NaN
10	6.344604	905.096680	9659	NaN
11	6.370034	1280.000000	16745	NaN
12	6.542396	1810.193360	25450	NaN
13	6.591412	2560.000000	29348	NaN
14	6.745217	3620.386720	27663	NaN
15	6.651652	5120.000000	25641	NaN
16	6.451523	7240.773439	26203	NaN
17	6.697566	10240.000000	25447	NaN
18	6.966520	14481.546879	26786	NaN
19	7.469420	20480.000000	31023	NaN
20	8.762968	28963.093757	26464	NaN

The second output is the dataframe of optimized model parameters (range, sill, and possibly smoothness) for a sum of gaussian and spherical models:

df_model_params

	model	range	psill
0	gaussian	66.897059	5.961545
0	spherical	28963.093757	2.113818

The third output is the spatial correlation function with spatial lags, derived from the variogram:

for spatial_lag in [0, 100, 1000, 10000, 30000]:
    print(
        "Errors are correlated at {:.1f}% for a {:,.0f} m spatial lag".format(
            spatial_corr_function(spatial_lag) * 100, spatial_lag
        )
    )

Errors are correlated at 100.0% for a 0 m spatial lag
Errors are correlated at 26.1% for a 100 m spatial lag
Errors are correlated at 24.8% for a 1,000 m spatial lag
Errors are correlated at 13.2% for a 10,000 m spatial lag
Errors are correlated at 0.0% for a 30,000 m spatial lag

We can plot the empirical variogram and its model on a non-linear X-axis to identify the multi-scale correlations.

xdem.spatialstats.plot_variogram(
    df=df_empirical_variogram,
    list_fit_fun=[xdem.spatialstats.get_variogram_model_func(df_model_params)],
    xlabel="Spatial lag (m)",
    ylabel="Variance of\nelevation differences (m)",
    xscale_range_split=[100, 1000],
)

This pipeline will not always work optimally with default parameters: variogram sampling is more robust with a lot of samples but takes long computing times, and the fitting might require multiple tries for forms and possibly bounds and first guesses to help the least-squares optimization. To learn how to tune more parameters and use the subfunctions, see the gallery example: Estimation and modelling of spatial variograms!